Dislocation Modeling using GTdef(v4.0)

Sections of the GTdef model

(Clicking on section heads will return to the Table of Contents)

  1. Basic Introduction
  2. GTdef Code and How to Download it
  3. Background Theory
  4. The Input File
  5. Simple Planar Forward Model
  6. Inverting a Uniform Slip Model
  7. Inverting for Non-Uniform Slip
  8. Checkerboard Testing (forward and inverse of synthetics)
  9. Resolution Spread Evaluation
  10. Layered Models
  11. GTdef formats for Green's Functions
  12. Ingesting External Green's Functions
  13. References

  1. Introduction

    2. Manual developed by Derrick Murekezi and Andrew Newman


    GTdef is an implementation of the Okada (1985) dislocation model written by Lujia Feng, Ting Chen, and Andrew Newman, with codes translated from disl (by Peter Cervelli). Okada (1985) can describe the surface deformation associated with rectangular dislocations of most orientations, within a purely-elastic half-space, however we've further adapted the codes to allow for horizontally layered materials. Fault planes do require one edge to be horizontal. Dislocations can be described with dip-slip, strike-slip, and/or opening, and hence can be used to describe a range of processes including earthquake faulting, interseismic coupling, and planar fluid changes like magmatic dike inflation or groundwater withdrawal.


    The code is developed so that one could perform both forward models that predict ground deformation and inverse models that use data with errors and some modeling constraints to predict information about the source. The source in either case can be either simple rectangular slips along the plane, orthogonal to it or some combination of both.


    Requirements:
    1. Algorithms are written in Matlab and require the 'Parameter estimation' toolbox for inversions.
    2. If you wish to use parallel processors, your version needs to include parpool, which was implemented around 2015.
    3. For plotting GMT version 5 or 6.
    4. These additional toolboxes and software are needed for Quadtree/InSAR processing:
      • Image Processing Toolbox
      • Parallel Processing Toolbox (if you want faster computation using multicore processing)
      • Mapping Toolbox
      • Signal Processing Toolbox
      • grdwrite2.m from kylebrill @ GitHub

  2. Getting/Installing Code

      3. This Version: 4.0

    Set up Instructions:
    1. In the selected directory, to clone GTdef run 
      #this will create a copy of the code which you can pull to every time there is an update to the master git repository
git clone https://github.com/avnewman/GTDef.git
    2. Be sure the current version of the programs are in your path. You can check this using the path function, and add it using addpath. 
       # within matlab
> addpath('/path/to/GTdef/v4.0/stable/') %replacing with your actual path
    3. Additionally, create a separate directory to run examples and save files. Running Matlab calls in this directory will save your results in one place to be analysed later.

  3. Background Theory

    4. Kinematic Modeling:

    A very brief discussion of kinematic modeling methods used here should exist. This would include each Okada (1985) analytical models, the Wang et al (2003) layered method, and general injestion of Green's functions from other sources.


    Inverse Modeling:

    GTdef performs a bounded linear least-squares inversion of Green's functions to define the best-fitting set of models to describe a dataset with errors. The program uses the parameter optimization toolbox program called lsqlin (Matlab info on it). You can read more about it and general inversion methods from a number of books (including Santamarina & Fratta, "Discrete Signals and Inverse Problems" [2005], and Menke, "Geophysical Data Analysis" -- particularly chapters 3 & 4).


    While the simplified forward problem exists:

    (1)

    d = Gm
    where Okada (1985) describes the Green's function, G, that relates model parameters m, to the data, d. If data are numerous, and/or model parameters are greater than one, each can be written as a vector of size n and m, with the G being a matrix sized n x m.

    The inversion equation, where we try to solve for model parameters becomes:

    (2)

    Gm = d
    For a least-squares solution, the simplified inversion becomes:

    (3)

    mest = [GTG]-1GT d
    Because we expect there to be interdependence between adjacent model patches, we can describe an additional set of equations to apply to the inversion and regularize the final model. Every model patch mi can describe its model roughness as the Laplacian of that component of slip (e.g. ds, ss, ts). We will try to minimize that roughness for each slip component of the model, s, which here will be the same as m:

    (4)

    dp= 0 = κ∇2s
    where κ is the smoothing kernel. Furthermore, we combine the data weights and errors into a weighting matrix W. Now, incorporating the errors and weighting, the forward problem becomes:

    (5)

    d = Gm = [ Wiid 0 ] = [ WiiG κ∇2s ] m
    where the data and greens function matrix are now everything in their respective matrices above. The diagonal components of the weighting matrix Wii = (wi)0.5/ei, which are the per datum weighting wi and errors ei. With d and G now containing the smoothing and weighting terms, our model estimate can now be defined as:

    (6)

    mest = [GTG+ ε2I]-1GTd
    where ε2I = κ∇2s. We can simplify this by defining the Generalized Inverse Matrix:

    (7)

    G-g = [GTG+ ε2I]-1GT
    so:

    (8)

    mest = G-gd
    The above mathematical formulation is modified for the bounded conditions used for the parameter estimation in lsqlin, including the option of positivity constraints, which make the full formulation much more complicated. However, the grouping of terms are important particularly for the development of distributed slip models as input into the solver, and for understanding the model resolution matrix and ultimately resolution spread (an estimate of parameter importance).

  4. The Input File

    5. The code includes a detailed input file (click here to download/view) that describes the structure of the input file for both the foward and inverse models. The file describes the model parameters and how they differ for different models run. Below we have included snapshots of the input file for each example model.

    Ground rules for the input file include:

    1. Model parameters and data are combined in one input file.
      1. Forward and inverse models are mixed and distinguished by the range [min max]. If parameter min == max (e.g. 0 == 0), then the parameter is fixed
      2. Output files can be, and are often used as subsequent input files. For example, an inversion will produce model parameters that you may want to use to predict deformation away from the data that were used in the inversion.
    2. No specific order is required for specifying parameters
    3. The first column is important to identify the data type. Flag is not case sensitive.
    4. Information within parameter rows are all white-space separated.
    5. All parameters use the same units, defaulting to meters for each length of fault components, slip magnitudes, and measurement data.
    6. Angles are described in degree
    7. Depths are too reported in meters and are increasing going into the earth.
    8. Any line preceded by a hash '#' is treated as a comment and is ignored.
    9. The only requirements for the most simple input file are at least one fault line, and one 'data' line, describing the parameters for each. All lines are characterized by their first field and the line order does not matter.
    In the following sections we will further explore parameter characterization within the input file.

    FAULT characterization:

    Each fault must fall into one of the below 7 categories described by the nature of slip on the fault, fault parameters, external geometries, or simply extrenal Green's functions. A fault line may look like (example shown in above-linked input file): 
    #fault type name        lon       lat     z1  z2   len   str   dip     ss     ds   ts     ss0  ssX      ds0  dsX      ts0  tsX    Nd  Ns
fault  1    gnrc-1      -120.2000 38.0000 3e3 15e3 100e3 170.0 25.0    2.5e-3 1.2  0      0    0        1    1.5      0    0      1   1   # inverted only on dip-slip between 1 and 1.5 m
    Depending on the fault type (second column) the fields within the row will vary.
    • FAULT Types method used to describe fault [1-4], external geometries [5-6], or external Green's functions [7]
      • 1 = uniformly or distributed slipping fault defined by one endpoint, fault length, and strike (ss ds ts)
      • 2 = uniformly or distributed slipping fault defined by two endpoints (ss ds ts)
      • 3 = uniformly or distributed slipping fault defined by one endpoint, fault length, and strike (rake rs ts)
      • 4 = uniformly or distributed slipping fault defined by two endpoints (rake rs ts)
      • 5 = external geometry with (ss ds ts)
      • 6 = external geometry with (rake rs ts)
      • 7 = external green functions
      Note: distributed slipping faults are followed by subfault definitions; slip values for the main fault are used for unspecified subfaults
    • The fault model defines a fault by its location in terms of longitude then latitude (or x then y if using a local coordinate system), its depth, strike and dip, slip parameters, and the number of subfaults within the model.
    • FAULT Parameters (for fault type 1)
    • flt = [ lon lat z1 z2 len str dip ss ds ts ss0 ssX ds0 dsX ts0 tsX ]
      • lon,lat (or xx,yy) - one endpoint describing the surface projection of the faults in either geographic (default), or a local cartesian coordinate system
      • z1 - vertical burial depth, describing top of slipping portion of fault [≥0]
      • z2 - vertical locking depth, describing the bottom of slipping fault [≥0]
      • len - fault length [≥0]
      • str - strike from the endpoint describe above (degree CW from N) [0-360]
      • dip - downward from horizontal, and right looking in the strike-direction [0-180]
      • ss - strike-slip motion (left-lateral +)
      • ds - dip-slip motion (thrust +)
      • ts - tensile motion (opening +)
      • ss0,ds0,ts0 - lower bounds for slips
      • ssX,dsX,tsX - upper bounds for slips
      • nd,ns - number of subfaults along-dip, and along-strike

    Data characterization:

    Every input file needs to desribe either real data, or points in which you want to predict the surface motions. Each data line begins with its unique identifying name describe below. A data line for 3-component GPS point data may look like (also from above-linked input file): 
    #point type name    lon       lat     z            Ue   Un   Uv      eUe  eUn  eUv	weight
point  3    rdom    -118.8979 37.6770 2417.4049    9.6  1.1  36.1    1.0  1.0  1.3	1
    • Data Types
      Depending on data type both the data type identifier (first column) and the data-type number (second column) will change as described below..
      • point - data described at a single point at the surface (e.g. GPS).
        Point-types are:
        • 1 = vertical component only
        • 2 = east, and north components
        • 3 = east, north, and vertical components
      • los - a 1-D data point of arbitrary orientation (e.g. line-of-site to SAR satellite).
        LOS-types are:
        • 1 = displacement in direction of LOS (e.g. toward satellite)
        • 2 = phase change in LOS direction (not implemented yet)
      • baseline - a baseline defined between two sites.
        baseline-types are:
        • 1 = length change only
        • 2 = east, north, and vertical components
        • 3 = east, north, vertical,and length change components
      • profile - a line defined by two endpoints with evenly distributed data points.
      • grid - a parallelogram defined by the lower-left (lon1,lat1) and upper-right (lon2,lat2) corners with data points parallel to the sides.
      Note: profile and grid are generally used for displaying results from a forward model.
    • Data Parameters
      The data-types described above will use differing parameters. Their meaning and convention are describe here.
      • lon(x),lat(y),z - horizontal location and elevation (positive upward) [m]
      • Erot,Nrot - rotation angles for the East and North axis of grid [degree; + CW] (-90 90)
      • Ue,Un,Uv - surface displacements in East, North, and Vertical directions [m]
      • Ul - length change between two sites [m]
      • ULOS - surface displacement in LOS direction [m]
      • eUe,eUn,eUv,eUl - standard error for displacements and length change [m]
      • eULOS - standard error for surface displacement in LOS direction [m]
      • LOSdirE,LOSdirN,LOSdirV - unit vector pointing from the ground toward the satellite (LOS direction)
      • N,Ne,Nn - number of data points, and number of columns and rows
      • wavelength - wavelength of signal for LOS (1/2 the SAR satellite natural wavelength)[not yet implemented]
      • weight - weight for incorperating different type of data {1}

    Other Model Parameters:

    To be desribed (e.g. coord, smooth, greensfns, matfile, resolution)

  5. Simple Planar Forward Model

    6. We'll start with the most straight-forward case of a single vertical fault plane with strike-slip motion on the interface.

    Example Forward Model Run:

    The simplist model includes just one fault and one data-point ran in a forward sense to prediction deformation at that data-point. We will not stray significantly from there.

    Input:

    1. We will create a vertical planar fault approximately 20 km long, with 1 meter, strike-slip motion, buried between 5 and 15 km depth. The output will describe the spatial deformation every 2 km across a 60x60 km grid surrounding the fault.
    2. To keep the algorithm from attempting an inversion, it is important that all slip parameter ranges for a given slip-type on a fault block have equal value (i.e. ss0=ssX, ds0=dsX, and ts0=tsX in this example).
    3. If all range values are set to zero '0', the initial value will be used. Here, we will have 1m of left-lateral (+) strike-slip that will not vary (all range parameters are set to zero).
    4. Input files should all end in .in
    5. The input file can be created in your favorite text-editor (e.g. vim). For simplicity here, we'll just direct stdout from an echo-command into a file called local1.in. The % represents a shell prompt. 
      % echo "
coord local # otherwise it will expect geographic coordinates
#fault type name       lon1 lat1   lon2  lat2  z1  z2    dip  ss  ds ts ss0 ssX ds0  dsX  ts0  tsX   Nd  Ns
fault  2    myfault    0   -10e3   0     10e3  5e3 15e3  90   1   0  0  0   0   0    0    0    0     1   1
#grid name    Erot Nrot lon1(x1) lat1(y1) lon2(x2) lat2(y2) Ne Nn
grid  1kmx1km 0    0    -30e3    -30e3    30e3     30e3     31 31
" > local1.in

    Run:

    1. To run GTdef, you must call up matlab (interactive and gui are not necessary).
    2. The processing code that oversees both forward and inverse models is GTdef and is called with just the input file name, and optionally, the number of processors you'd like it to use on your machine. By default, it will use all available processors if not defined. 
       # within matlab
> GTdef('local1.in',1) % will run on '1' core.

    Output:

    1. This will create an output file called 'local1_fwd.out' that will repeat the model, and give predicted results for the defined grid locations (now as 'point' data-type).
    Plotting results:
    1. Quick and dirty visualization can easily be achieved using the freely available gnuplot program. This allows us to look at the full 3D vector field. 
       # first comment out all lines that are not output data using vim or similar. (not shown)
 % gnuplot
   gnuplot>  set ticslevel 0.0 # removes empty whitespace below plot 
   gnuplot>  splot 'local1_fwd.out' u 4:5:(0):($7*1e5):($8*1e5):($9*1e5) w vect t "surface displacement"  # just the surface results amplified to see variability
   #If you're more adventurous, you can plot the fault too (this assumes the fault is vertically dipping).
   gnuplot>  splot "< awk '$1==\"point\"{print $0}' local1_fwd.out" u 4:5:(0):($7*1e5):($8*1e5):($9*1e5) w vect t "surface displacement",\
   "< awk '$1==\"fault\"{printf \"%f %f %f\\n%f %f %f\\n%f %f %f\\n%f %f %f\\n%f %f %f\\n\", $4,$5,-$8,$6,$7,-$8,$6,$7,-$9,$4,$5,-$9,$4,$5,-$8}' local1_fwd.out" w l lw 2 lt -1 t "fault"
  # use the cursor to move around the data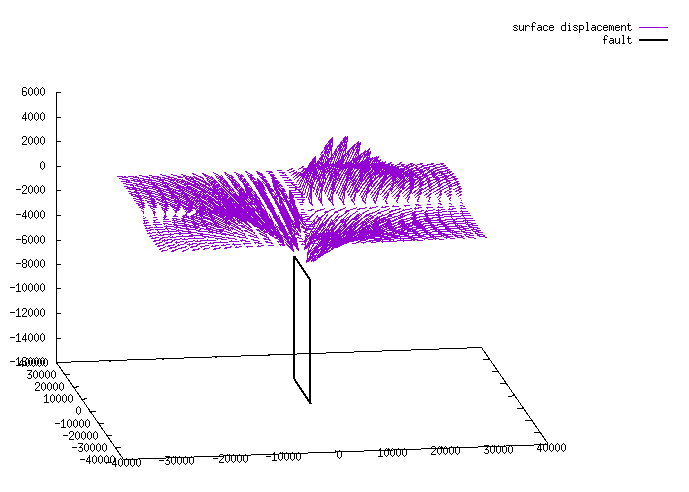

  6. Inverting a Uniform Slip Model:

    7. (from 'examples/Uniformslip/Solomon')

    Input:

    We will need to build the model, including gathering the appropriate data and then estabishing an appropriate a priori interface. In this example, we will use the very small tsunami earthquake described in Newman et al. (2011).
    1. Data: Here, we pull coastal subsidence data from sheet 3 of the excel spreadsheet. The data, being just vertical uplift/subsidence data need to be convert into the 'point 1' format in GTdef. Errors are estimated to be approximately 0.1 m on all data (assuming error in tidal correction and prior high-tide estimates), Because all data were measured using the same methods and likely have similar error values, we choose to give them all equal weight. 
      #point type name                        lon             lat        z    Uv     eUv   weight
point 1  Rendova-Rendova_Harbor         157.33602       -8.40359   0.0  -0.15  0.10  1.0
point 1  Rendova-Epata_Creek            157.30622       -8.43730   0.0  0      0.10  1.0
point 1  Rendova-Mbaniata               157.26260       -8.63325   0.0  -0.70  0.10  1.0
point 1  Rendova-Hofofo_Pt              157.19633       -8.56530   0.0  0      0.10  1.0
point 1  Rendova-Habila                 157.22920       -8.60414   0.0  -0.60  0.10  1.0
point 1  Rendova-Rava_Pt                157.40336       -8.72264   0.0  -0.60  0.10  1.0
point 1  Tetepare-Tofa                  157.53432       -8.75576   0.0  -0.40  0.10  1.0
point 1  Tetepare-Jetty_near_Ecolodge   157.44286       -8.72234   0.0  -0.25  0.10  1.0
point 1  Tetepare-Ecolodge_boat_ramp    157.44321       -8.72120   0.0  -0.30  0.10  1.0
point 1  Rendova-Rano                   157.32886       -8.62969   0.0  -0.50  0.10  1.0
point 1  Rendova-Vankuva                157.33953       -8.60934   0.0  0      0.10  1.0
point 1  Rendova-Kofi_Bay_village       157.33874       -8.6039    0.0  -0.40  0.10  1.0
point 1  Rendova-Mauru_Loging_Camp      157.39881       -8.5137    0.0  -0.30  0.10  1.0
point 1  Rendova-Ugele                  157.39921       -8.44959   0.0  0      0.10  1.0

    2. Modeled Fault: We need to come up with a choice for the appropriate input model. This can be done using existing published fault geometries, evaluating distributions of microseismicity, focal mechanisms, examination of surface topography/bathymetry, or some combination of these methods. Once an initial model is chosen, output from a number of inversions using differing geometries can be used to chose an optimal geometry by evaluating each geometry's overall model fit. The output results of these inversions can then be broken up into distributed models (discussed below). Here, Newman et al. (2011) defined the fault using a combination of the overall fault strike, and testing a range of dip geometries.


      For our inversion, we will define a finite range of allowble thrust(+) values (ds, and dX between 0 and 100 m). Because data here are only vertical, we will chose to set strike-slip to 0 and not allow it to vary in the model, as this component will be very poorly constrained, possibly being dependent on choice of geometry. Finally, because this is a uniform slip model, the number of slip and strike components must be set to one (Nd=Ns=1).

      Note: Here, the dip =158° for a strike of 125°. This is equivelent to a dip of 22° striking 305°, but from the far end-point.

      #fault type name lon      lat     z1  z2   len   str   dip   ss ds ts ss0 ssX ds0 dsX  ts0 tsX  Nd  Ns 
fault  1    slm  157.0990 -8.6920 0   5200 50000 125.0 158.0 0 0.1 0  0   0   0   100  0   0    1   1

    Run:

    After combining the above parameters into a single input file (e.g. 'solomon.in'), you can run the code just as was done in the forward model.

    Output:

    1. Output files: If the model converges, you can analyze the output results in either the '_inv.out' or '_kp*.out'. The former file gives the fit results of the run, while the later gives the model results as well as their predicted displacements at the sites described in the orginal input model. Its this second file that can be used as an input for future runs.
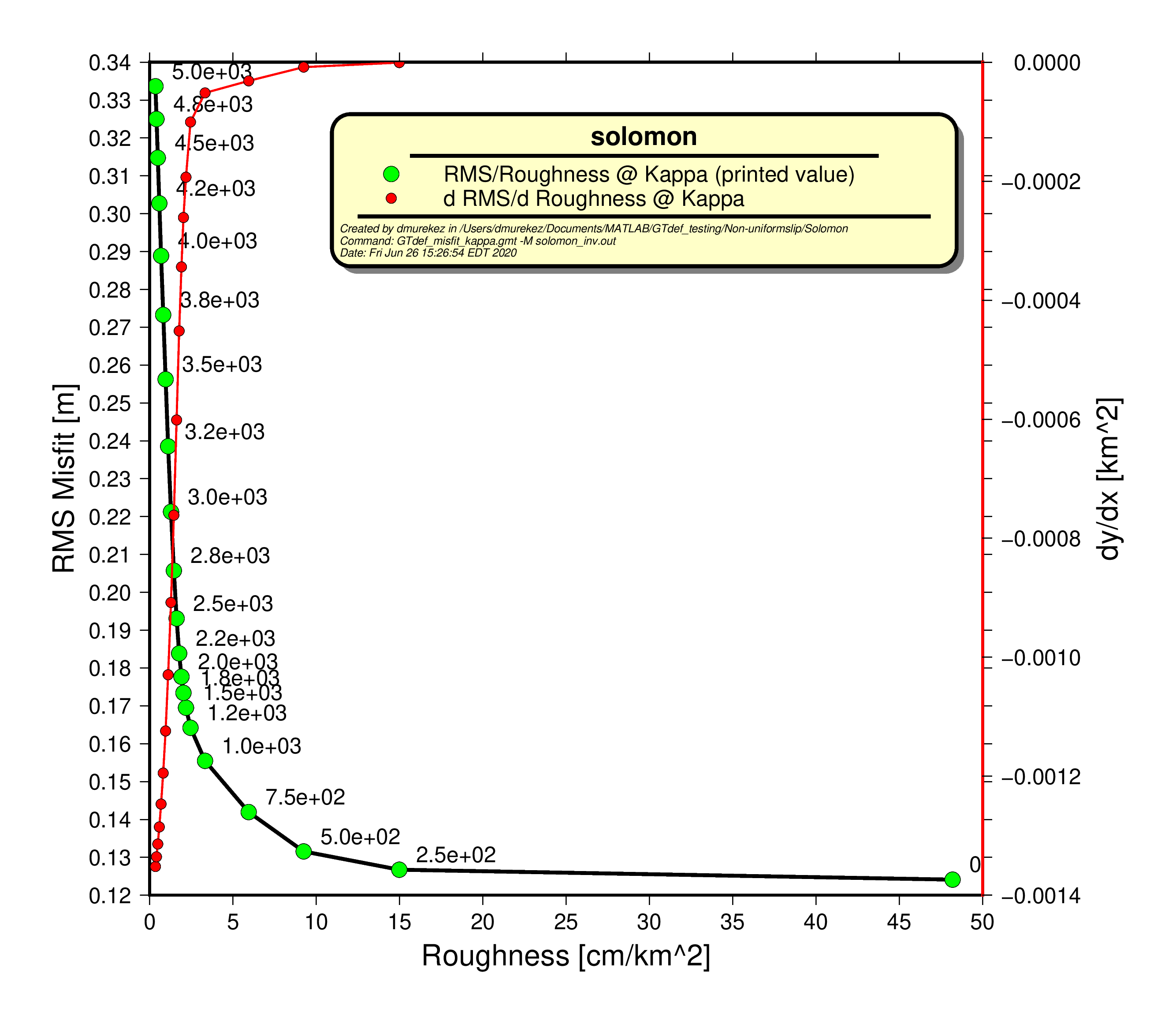
      • Model fit: Below is the output from 'solomon_inv.out' created by GTdef. Since there is only one inversion ran, there will be only one data line following a header line preceded by its column number (#). 
        #(1)beta (2)kappa (3)data_num (4)slip_num (5)ndf (6)rss [m^2] (7)rms [m] (8)wrrs [m^2] (9)wrms [m] (10)chi2 (11)rchi2 (12)r_1d [cm/km] (13)r_2d [cm/km^2] (14)strain [cm/km]
0.00000e+00  0.00000e+00      14 1 13 4.05607e-01  1.70211e-01   4.05607e+01   1.70211e+00   4.05607e+01   3.12005e+00   NaN           NaN           NaN
      • Model results and predicted displacements: Shown here is the output from 'solomon_kp0.00000.out'. Note that in addition to lines repeating the input file, there are several default input options explicitely written out here (e.g. coord, earth, surface). Also included are model misfits repeated from the above file. Lastly, the model line now includes the model output for a best-fit (showing 5.16091 m of thrust), and the model predictions for each data line (e.g. Rendova-Mbaniata predicts 62.62 cm of subsidence).Though data type was input as point 1, they are output as point 3, giving the predicted horizontal motions as well. Errors are not reported for models. 
        coord   	geo
#data_num	14
#slip_num	1
#ndf     	13
#rss      	4.05607e-01  [m^2]
#rms      	1.70211e-01  [m]
#wrss   	4.05607e+01  [m^2]
#wrms   	1.70211e+00  [m]
#chi2    	4.05607e+01
#rchi2   	3.12005e+00
#r_1d   	NaN          [cm/km]
#r_2d   	NaN          [cm/km^2]
#strain   	NaN          [cm/km]

earth	homogeneous	3.00e+10  	0.2500

kappa   	0.00000
beta     	0.00000

smooth   	2d
surface  	free

fault 1 slm  157.09900000   -8.69200000  0.0000e+00   5.2000e+03 5.0000e+04   125.00 158.00     0.00000 5.16091  0.00000   0.0000 0.0000  0.0000 100.0000  0.0000 0.0000    1 1
point 3 Rendova-Rendova_Harbor	  157.33602000  -8.40359000  0.00000e+00    -0.09951   -0.25301    0.00474         NaN        NaN        NaN  1.00
point 3 Rendova-Epata_Creek	  157.30622000  -8.43730000  0.00000e+00    -0.11693   -0.31236   -0.00387         NaN        NaN        NaN  1.00
point 3 Rendova-Mbaniata	  157.26260000  -8.63325000  0.00000e+00    -0.89590   -1.40681   -0.62620         NaN        NaN        NaN  1.00
point 3 Rendova-Hofofo_Pt	  157.19633000  -8.56530000  0.00000e+00    -0.26215   -0.92622   -0.30033         NaN        NaN        NaN  1.00
point 3 Rendova-Habila	  157.22920000  -8.60414000  0.00000e+00    -0.70254   -1.31715   -0.55581         NaN        NaN        NaN  1.00
point 3 Rendova-Rava_Pt	  157.40336000  -8.72264000  0.00000e+00    -0.98978   -1.39069   -0.60162         NaN        NaN        NaN  1.00
point 3 Tetepare-Tofa	  157.53432000  -8.75576000  0.00000e+00    -0.71027   -0.73619   -0.19750         NaN        NaN        NaN  1.00
point 3 Tetepare-Jetty_near_Ecolodge	  157.44286000  -8.72234000  0.00000e+00    -0.87663   -1.18799   -0.39089         NaN        NaN        NaN  1.00
point 3 Tetepare-Ecolodge_boat_ramp	  157.44321000  -8.72120000  0.00000e+00    -0.86957   -1.17774   -0.38133         NaN        NaN        NaN  1.00
point 3 Rendova-Rano	  157.32886000  -8.62969000  0.00000e+00    -0.73815   -1.12756   -0.30286         NaN        NaN        NaN  1.00
point 3 Rendova-Vankuva	  157.33953000  -8.60934000  0.00000e+00    -0.59654   -0.93641   -0.17707         NaN        NaN        NaN  1.00
point 3 Rendova-Kofi_Bay_village	  157.33874000  -8.60390000  0.00000e+00    -0.57048   -0.90517   -0.16057         NaN        NaN        NaN  1.00
point 3 Rendova-Mauru_Loging_Camp	  157.39881000  -8.51370000  0.00000e+00    -0.24266   -0.41934   -0.00177         NaN        NaN        NaN  1.00
point 3 Rendova-Ugele	  157.39921000  -8.44959000  0.00000e+00    -0.15468   -0.29970    0.00941         NaN        NaN        NaN  1.00
    2. Predicting displacements elsewhere: To estimate model displacements outside of the original data points in '_kp*.out', you can copy the model output into a new file along with the points that you want prediced. Here, we are just using a grid, similar in the foward model example above, name it something like 'solomon_fwd.in', and run as before. 
       #fault type name lon      lat      z1         z2       len        str    dip     ss    ds     ts      ss0   ssX    ds0   dsX   ts0   tsX    Nd  Ns 
fault 1    slm  157.09896 -8.69204 0.00e+00   5.20e+03 5.00e+04   125.00 158.00  0.000 5.167  0.000   0.00  0.00   0.00  0.00  0.00  0.00   1   1
#grid name        Erot Nrot lon1    lat1    lon2     lat2     Ne    Nn   
grid  Solom_region   0    0    156.4   -9.3    158.1    -7.9     200   200
    Plotting results:
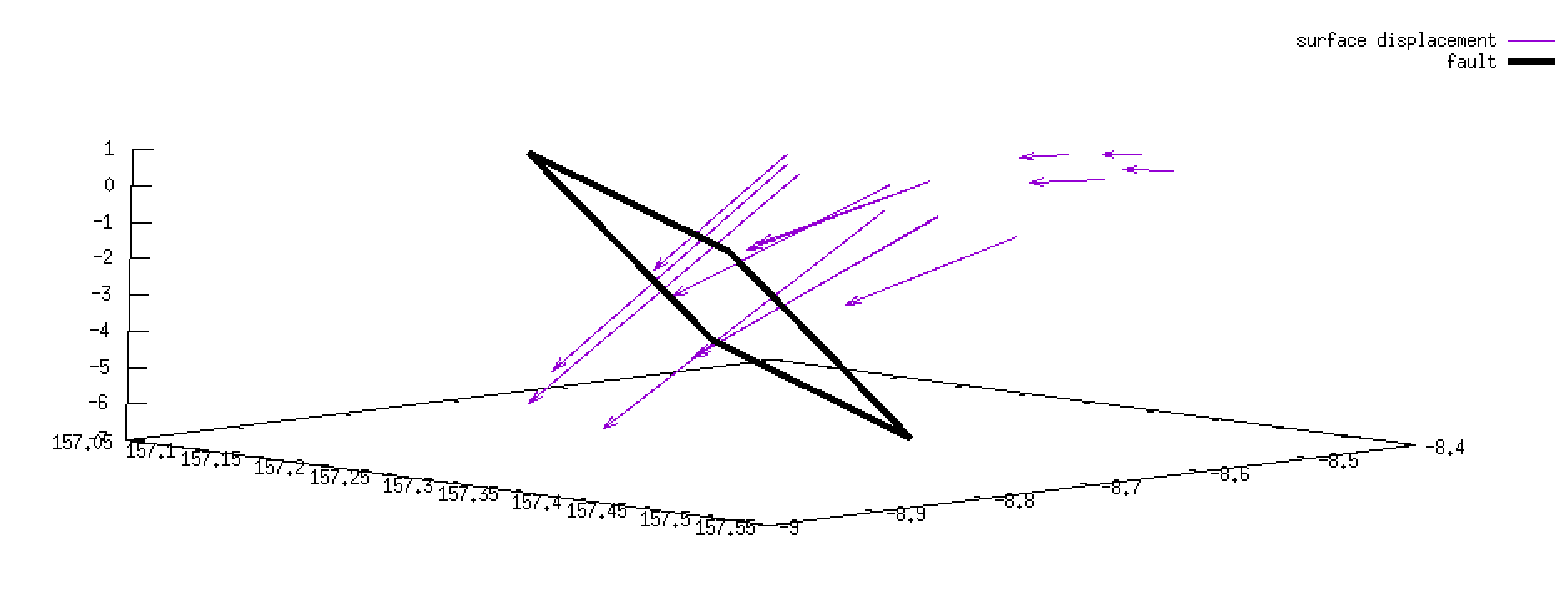
    1. One tool that is particularly useful is the supplied algorithm 'GTdef_project', as it can take the predicted output model and transform it into a highly-readable file for your favorite plotting program. 
      > % within matlab
> GTdef_project('solomon_kp0.00000.out')
      This creates a new file (here 'solomon_kp0.00000_patches.out') that describes all elements (here only one) of the model, including geographic position of corners, the element center position, and slip values. While you could use a more full-featured plotting program like GMT, we'll again use gnuplot for our quick and dirty plot to show the predicted displacements from '_kp*.out', and then model geometry from '_kp*_patches.out'. 
      # within gnuplot 
# Note: We are using diffential scaling of the displacement vectors to scale with the geographic position and depth (in degrees° and km) 
gnuplot> splot "< awk '$1==\"point\"{print $0}' solomon_kp0.00000.out"\
u 4:5:(0):($7*1e-1):($8*1e-1):($9*1e1) w vect t "surface displacement",\
"< awk '$1==\"slm\"{printf \"%f %f %f\\n%f %f %f\\n%f %f %f\\n%f %f %f\\n%f %f %f\\n\", $4,$5,-$6/1000,$7,$8,-$9/1000,$10,$11,-$12/1000,$13,$14,-$15/1000,$4,$5,-$6/1000}' solomon_kp0.00000_patches.out"\
w l lw 4 lt 7 -8 t "fault"
    2. After using your pointer to move around your model appropriately, your result should look something like this:


  7. Inverting for Non-uniform Slip:

    8. (from 'examples/Non-uniformslip/Solomon')

    This problem is a little more tricky, as we will quickly go from an overdetermined problem (more data than model paremeters), to an underdetermined problem. In order to get around this, and to solve for realistic slip, we constrain the interdependence between individual slip patches. The most popular way to do this is to define minimize the 'roughness' of the slip patch, as defined in Harris and Segall (1987), but more concisely in Jónsson_et al_(2002).
    The method works to minimize the 2D second-order derivative of the slip surface so that large changes are constrained within a certain value. The way it's been implemented here is that a series of roughness solutions are determined, all yielding different misfits to the data. It is a somewhat arbitrary decision to chose the optimal roughness parameter. Usually this is done by evaluating the kink-point by which additionally smooth results significantly increase misfits.

    Input

    1. Choose your kappa value (parameter that controls roughness) to range between 0 to 5000 by 500. 
      kappa 2 0  5000 11
    2. Setup your fault to now have 70 subfaults, 7 patches along-strike and 10 patches along-dip. 
      #fault type name   lon       lat     z1  z2    len    str    dip     ss   ds    ts    ss0  ssX    ds0  dsX    ts0 tsX    Nd  Ns
 fault  1   slm    157.0990  -8.6920  0  5200  50000  305.0  22.0   0    0.1   0     0    0      0    100    0   0      7   10

    Run

    1. Within Matlab, run GTdef('solomon_inv.in') like in the example above except this time you're running an inversion due to the way the fault parameters are set up.
    Output
    1. This time, you have two kinds of output files, those that end in '_kp*' correspond to each kappa value you set in step "i" above, and the other is a summary file '_inv.out'. The inversion summary file will be used in the next step to determine the optimal smoothing factor (kappa value) for this dataset.
    2. Explore your inversion results. Using GTdef_misfit_kappa.gmt, try plotting misfit vs. roughness to see how your choices in kappa affect these results. Looking at the L-curve, the 4th lowest kappa value is optimal for this example dataset. 
            # in shell (command line)
      GTdef_misfit_kappa.gmt -M nicoya_camp_inv_inv.out


    Plotting results:
    1. Finally, once you've chosen your optimal kappa value, run a new forward model, and repredict deformation. The new forward model input will be a modified version of the corresponding '_kp.out' file to the optimal kappa value determined from the step above. Remember, for a forward model, it is important that all slip parameter ranges for a given slip-type on a fault block have equal value (i.e. ss0=ssX, ds0=dsX, and ts0=tsX).
    2. You might want to look at your results in a geographic reference system. We've created a GMT script (GTdef_slipmodel.gmt) to do this, but you may need to modify it for your purposes. 
                   # in shell (command line)
             GTdef_slipmodel.gmt -M solomon.in -K750 -R157.0/157.7/-9/-8.3 -S0.1/1/0.1 -D
      Here is an example of a plot from the results obtained with an inversion with kappa=750.

  8. Checkerboard Testing:

    9. Here we will create synthetic input models that we will invert for using realistic noise to identify the types of features that we may be able to see given the model, data geometry and quality. This is from 'examples/Non-uniformslip/Nicoya/Checkboard'.

    Develop a Synthetic Forward Model:

    1. Define the size boxes that you will want to try to recreate in your checkerboards. As a general rule, we find that the model patch size that you can interpret is dependent on and about equal to its depth relative to stations overhead. This assumes stations are immediately overhead. This will certainly change as a function fault dip, and station coverage, thus while you may have theoretical fidelity to recover even extremely small patches near the trench (where the fault is just below you), you may not have data until you're on land, 50 to 200 km away. Thus, we will take an initial example of a fault patch that is 50 km laterally from a 20° dipping fault surface, the checkerboard patch should be around 50km*sin(20°)=17km . At 100 km, it's about 34 km, and at 200 km it's about 70 km, assuming constant dip. Note, that this is just a starting and approximate parameter.
    2. You will now need to define a number of subfaults that match your expected optimal resolution. This too can be done by hand, but the program, GTdef_ckbd_subflt.m makes it much easier. Check out the header notes within the program for details.
    3. For a fault named 'nicoya' with 30x40 patches and approximately 200 km x 200 km in size, you can run 
              % within matlab
        GTdef_ckbd_subflt('nicoya',30,40,3,4, [0 -.0823 0  0 0 0 0 0 0],[0 0 0  0 0 0 0 0 0])
      to define a fault that groups alternating blocks into 3 along dip, and 4 along strike patches. Here, the the blocks are 20x20 km (smallest size for coastal data--this is too small for deeper patches). The vectors here define the forward behavior of the patches that we normally think of as 1's and 0's. So, patch 1 (the black, or slipping patch), p1= is only backthrust at 82.3 mm (no inversion set for these patches). For patch 0 (the white, or null patch), p0= zeros (9 of them). The program will create a file called GTdef_ckbd_subflt.out that will only contain the sub-fault parameters. This will need to be copied into your input model file that contains your fault characterization and 'points' in which you want to predict deformation for the forward run. 
              # in shell (command line)
        cat GTdef_ckbd_subflt.out >> nicoya_ckbd.in
    4. Once it's ready, run 
              % within matlab
        GTdef('nicoya_ckbd.in')
      If everything works you will get your initial noise-free synthetics.
    5. Using GTdef_slipmodel.gmt, plot the noise free model with the nicoya_ckbd_fwd.out (the output from the forward run). 
           # in shell (command line)
     GTdef_slipmodel.gmt -M nicoya_ckbd.in -S100/100/10
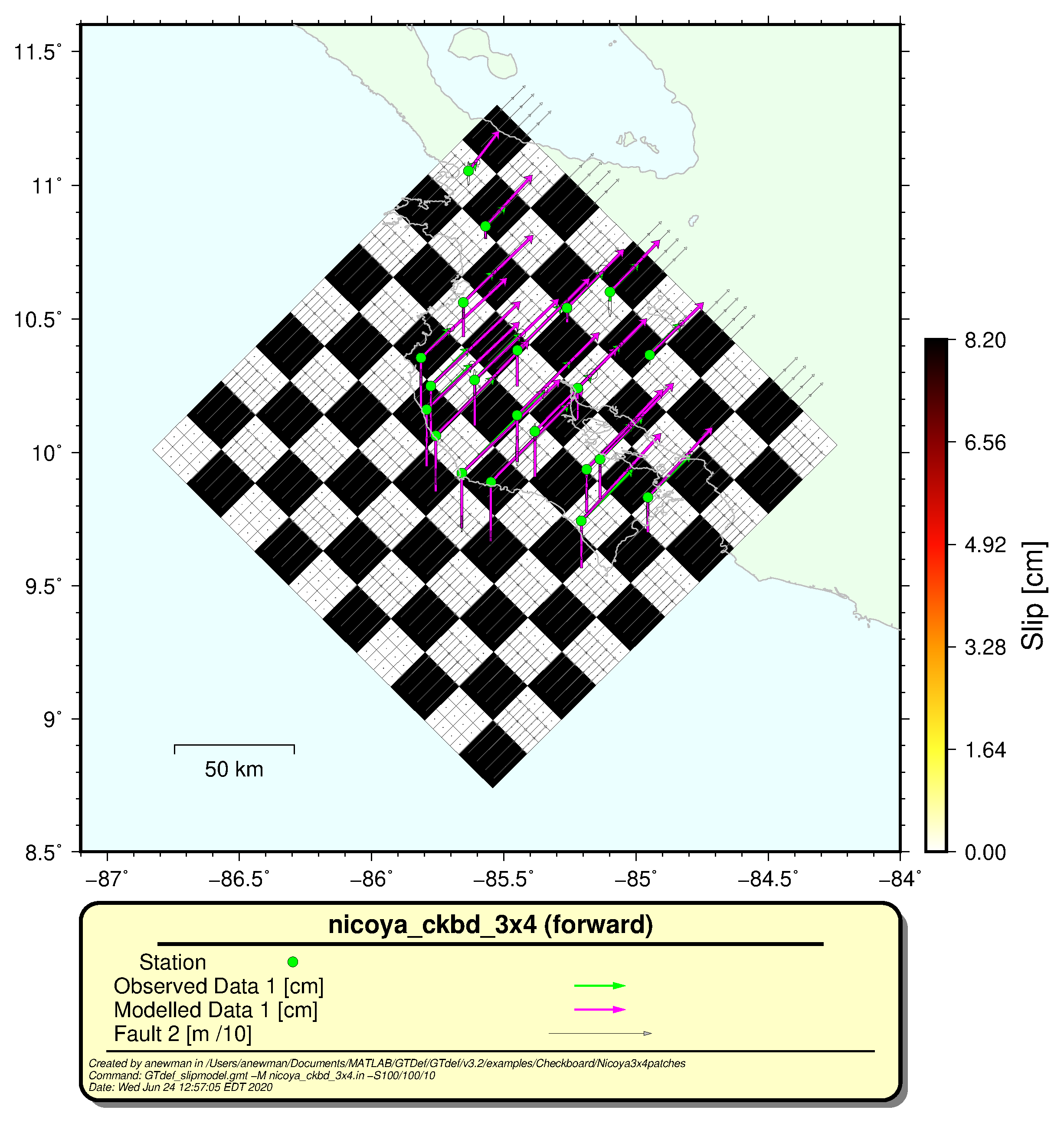
      The figure should look like the example below.



      Note, that because this program is written for real data, the labeling may not be accurate. Here, 'observed' is arbitrary, and whatever was in your original input file. Modeled data are the predicted results that will be used for subsequent inversions.

    Adding Noise:

    Good synthetic data includes an approximation of the noise that you'd get in the real data. For this, We've developed a simple shell script that searches only point data from an output file and adds Gaussian noise to the data itself. The program then writes out the perturbed data and error estimates representing the input error, of the size defined within the script. This program needs updating for easier and general use, but it's pretty easy to run, as is.

    1. Copy the program to your working directory (its called add_noise.sh and is in the plotting directory shared with the GTdef scripts).
    2. Edit the parameters at the top of the file to include the expected East, North, and Vertical noise in your data (in meters). Now run it it on the output file, directing into a new output. As an example: 
              # in shell (command line)
        add_noise.sh nicoya_ckbd_fwd.out > nicoya_ckbd_fwd_wNOISE.in
      Note that the directed output is now ending in '.in'.

    Inverting Synthetics:

    Here we will determine what the synthetic and noised data show on the fault.

    1. Edit new synthetic input file to either comment out or remove the sub-fault definitions, since the original prescribed specific slip values on sub-faults that we will instead try to find when we run the new inversion here.

      You can do this manually, or run a script:

              # in shell (command line)
        # this scrubs file directing it into a new file that then replaces the original.
        grep -v subfault nicoya_ckbd_fwd_wNOISE.in > j1 ; mv j1 nicoya_ckbd_fwd_wNOISE.in
    2. You can add or modify any other parameters that you want into the header of the file input file. We want to be sure that we're running a range of kappa values. Here it's 5 between 1000-5000, 5 between 7k and 15k, and 4 between 20k and 50k, but the useful range depends on the number of patches and relation to data.
      Modify nicoya_ckbd_fwd_wNOISE.in to include: 
                surface free             # slip to the trench here
          kappa 2 1000 5000 5      # 1k-5k for with n=5
          kappa 2 7000 15000 5     # every 2k now
          kappa 2 20000 50000 4    # every 10k now
          resolution 1             # output the results of the resolution matrix (we can use later)
          lsqlin 10 1e-10          # less iterations and higher tolerance limits (faster runs with no real degradation).
          project on               # runs through and creates easy to read geographically projected outputs of model and slip parameters.

      Change the fault line to invert (e.g. make thrust range from -0.823 to 0, the ds0 and dsX values). 
                 #fault is set for inversion (ds0, dxX = 0, -.0823)
           #fault type name    lon1         lat1       lon2         lat2         z1 z2      dip   ss  ds      ts ss0 ssX  ds0     dsX  ts0 tsX  Nd Ns
           fault  2    nicoya  -85.54233907 8.74026277 -86.82826920 10.01077299  0  6.2e+04 17.0  0   -0.0823 0  0   0    -0.0823 0    0   0    30 40
    3. Run the inversion: 
                % within matlab
          GTdef('nicoya_ckbd_fwd_wNOISE.in')
    4. Determine appropriate Κ value to use by evaluating the information in 'nicoya_ckbd_6x8_fwd_lowNOISE_inv.out', which can be plotted with GTdef_misfit_kappa.gmt. 
                # in shell (command line)
          GTdef_misfit_kappa.gmt -M nicoya_ckbd_3x4_fwd_lowNOISE_inv.out
      Results are here.
    5. Now, evaluate/visualize the results of the inversion to determine which patches have better or worse representation of the original input model that you created (your checkerboards). A great way to do this is to create very similar plots of both the result of the forward prediction (nicoya_ckbd_fwd.out) and the new inverse at the kappa that you feel most appropriate (e.g. nicoya_ckbd_fwd_wNOISE_k9000.out). Now the files should be ready for the helper program GTdef_slipmodel.gmt. 
                # in shell (command line)
          GTdef_slipmodel.gmt -M nicoya_ckbd_fwd_lowNOISE.in -K 9000 -S100/100/10
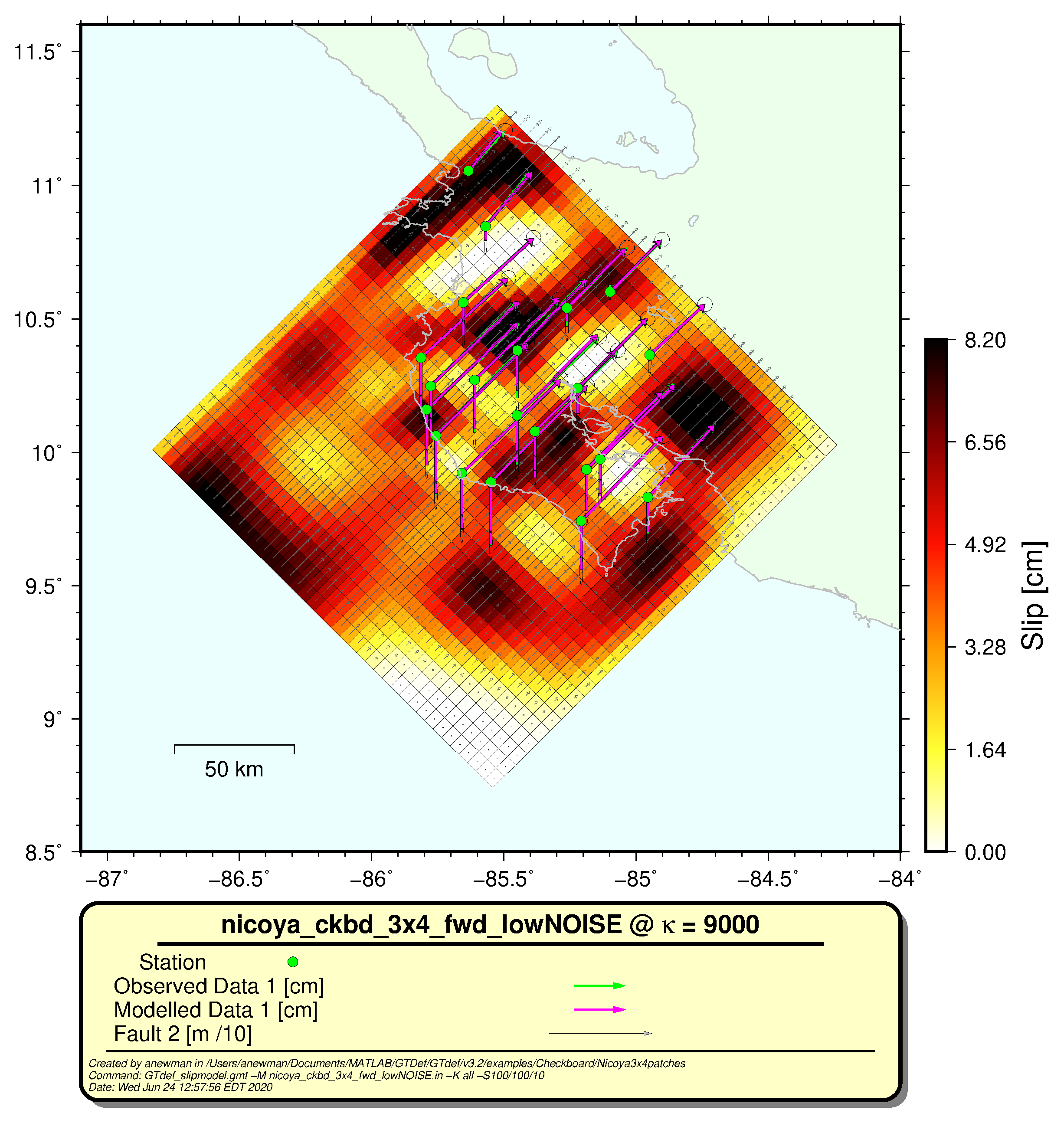
      The figure should look like the example below.

    Notes:

    1. As you can see in the above figure, the checkerboards are only replicated near the coast, and the predicted model becomes smooth with apparent larger patches both up-dip and down-dip, denoting loss of resolvability from a lack of stations immediately overhead (updip), and insufficiently large patches sizes (downdip).

      To improve on the down-dip problem, it is possible to make a hybrid checkerboard model with larger down-dip patches (maybe 40x40 km), to test the resolution of larger slip features. When doubling the patch sizes, features are much better resolved (in 'examples/Non-uniformslip/Nicoya/Checkboard/Nicoya6x8patches').

      1. input checkerboard
      2. trade-off curve
      3. inversion results

    2. Checkerboard testing is relatively straightforward, but a somewhat cumbersome problem with a visual and not very quantitative assessment of the model quality given data. Instead, it may be much better to look at the output of the resolution matrix, itself.
    3. The examples used in the checkerboard tests above use campaign data from the Nicoya Seismic Cycle Observatory GPS data.

  9. Resolution Spread Evaluation:

    10. Theory:

    If you've ran inversions with the 'resolution' flag set to one (see option in Checkerboard Testing section), we should have outputs with the tail '_patches_R.out' for each of the kappa values in our models. This file describes the output of the diagonals of the model resolution matrix, Rjj, as the product of the Generalized Inverse Matrix and the Green's function (see Theory section).

    (9)

    R = G-gG
    Equation(7) from above can be rewritten as:

    (10)

    G-g = [GTWeG+ ρWm]-1GTWe
    where Wm is the Laplacian of the slip, We is the error weighting matrix, and ρ is the roughness intensity applied to the models (Jonsson et al., 2002; Kyriakopoulos and Newman, 2016).


    From the diagonals of the resolution matrix, Rjj, you can get a characterization of how spatially a model patch's resolution is spread output across the model space. This can be related in a single scalar per patch that is dependent on the patch size. This parameter is called the resolution spread, rj, and is

    (11)

    rj = Lj / √Rjj,
    where Lj is the nominal patch size (Funning et al., 2005; Kyriakopoulos and Newman, 2016).

    Because R doesn't depend on the actual values of the data, but only its location and weighted errors, relative to the model, the same is true for rj.


    Evaluation:

    (from 'examples/Non-uniformslip/Nicoya/Checkboard')

    We've created a program that calculates Lj, and rj for a selected component of slip. The program GTdef_Rmodel.gmt uses similar inputs to GTdef_slipmodel.gmt, but requires Kappa (-K) and Slip components (-C) to be described. As noted above, the program requires the respective '_patches_R.out' files that are created with the c>'resolution' flag set to 1 before an inversion. 

       # in shell (command line)
   GTdef_Rmodel.gmt -M nicoya_ckbd_fwd_lowNOISE.in -K7000 -S D -D
    This will plot the dip-slip (-S D) component, at Κ=7000, displaying the result (-D).


    The figure should look similar to the example below.


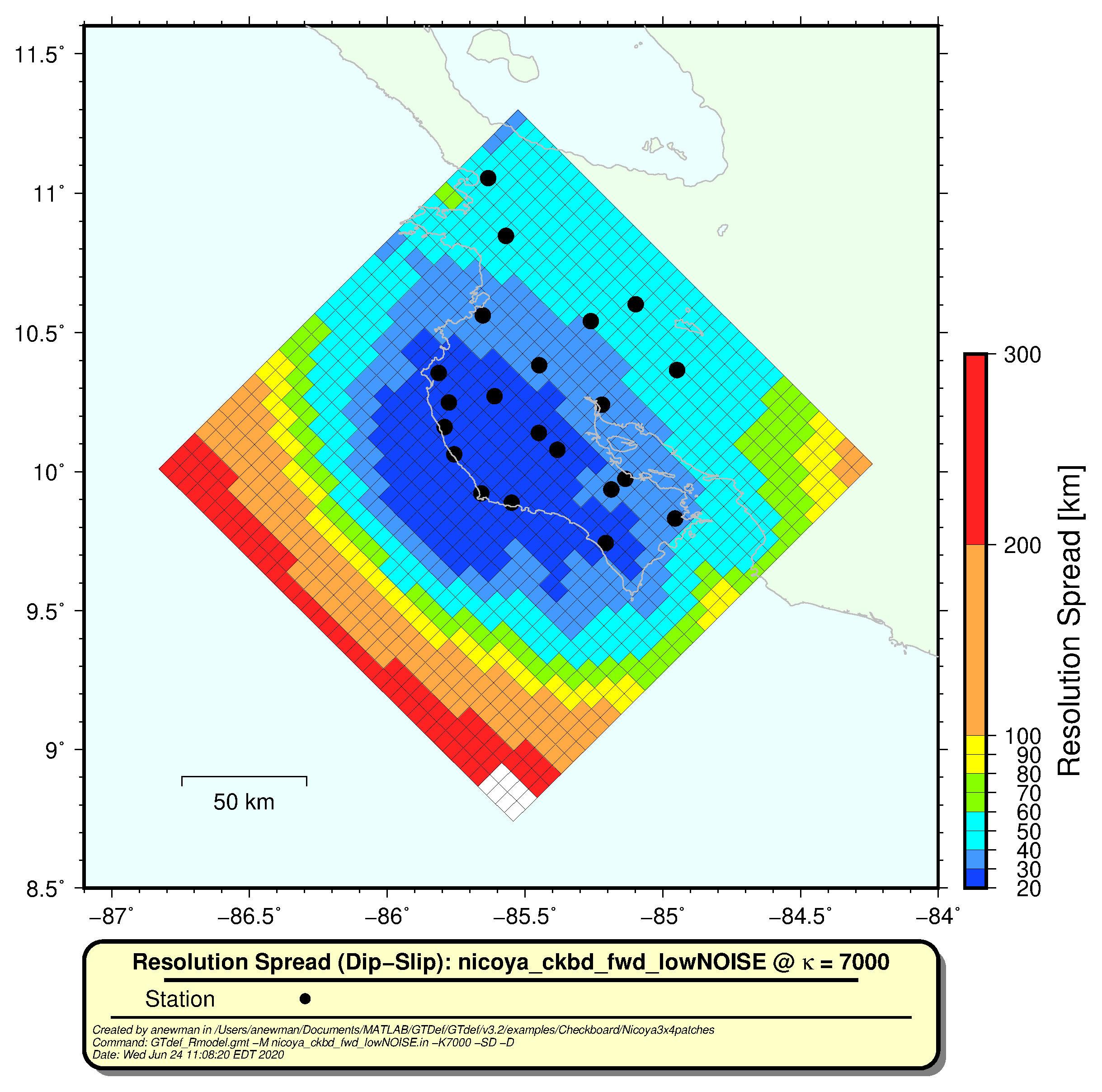
    The real beauty of the Resolution Spread is in it's simplicity and quantitative nature. Instead of creating apriori assessments of approximate resolvable model size, developing a model/running it, and doing "squinty-eyed" qualitative analysis of what you can resolve (as is done with Checkerboard testing), you get real numbers, with direct resolvable properties of patch size.


    While plotting rj gives a direct image of all patches average spread, you can use resolution 2 to get information on the off-diagonal components of the model resolution matrix to plot the actual spatial smearing of individual patches, per component (see Kyriakopoulos and Newman, 2016). You may need to develop your own plotting algorithm for this.

  10. Layered Models

    11. In the examples above, we've been working with a homogeneous elastic half-space. In this section, we will describe another set of algorithms for creating layered models within GTdef. The algorithms GTdef_edgrn.m and GTdef_edcmp.m, create the Green's functions and compute the expected deformation, respectively. The codes are adopted from Wang et al.(2003), originally written in FORTRAN.

    Input

    (from 'examples/Layered_Models/Nicoya/All_stations')

    To build an input file to run the layered model it is necessary to set the earth structure to be 'layered' and define appropriate parameters for the desired layers. Details are included in the example input file. The layer parameters are defined as follows; 
    # nl       - number of lines of layer information (!= number of layers)
#            each layer except the top layer (interface of halfspace) has two lines of records
#            if upper & lower values are different, layers will be treated as constant gradient
# obsz     - uniform depth of observation points [m]
# nr       - number of radial points for green functions
# minr     - minimum radial distance [m]
# maxr     - maximum radial distance [m]
# nz       - number of depth points for green functions
# minz     - minimum depth (positive points down) [m]
# maxz     - maximum depth (positive points down) [m]
# srate    - sampling rate for wavenumber integration
#             the ratio between the Nyquist wavenumber and the really used wavenumber
#             suggested value 10-128 {12}
#             the larger the value is, the more accurate the results are, more time required
#earth  layered  nl  obsz 	nr 	minr	maxr 	nz 	minz	maxz	srate
earth   layered  22  0.0	1201	0.0	300e3	326	0.0	65e3    12

    Run

    For this example, we use a combination of Campaign and Continuous stations from the Nicoya dataset. The layers are defined by Vp, Vs, depth and density (rho), in this example we use an initial 1-D best-fit velocity model specific to the region as published in DeShon et al.(2006). In this example, each layer has internally constant properties, and are described from shallowest to deepest. The bottom layer defines everything underneath it. Keep in mind that each line is the layer boundary conditions, and not conditions across the entire layer. A complete input file can be found in the examples directory (Layered_models). The first 5 lines are shown below: 
    #layer id     depth   Vp [m/s]    Vs [m/s]  rho [kg/m^3]
layer  1      0.0e3   5.35e3      3.01e3    2646.291
layer  2      5.0e3   6.12e3      3.44e3    2736.762
layer  3      5.0e3   6.12e3      3.44e3    2736.762
layer  4      9.0e3   6.12e3      3.44e3    2736.762
layer  5      9.0e3   6.12e3      3.44e3    2736.762
    After the model is set up, the model can be run the same way as other models: 
      % within matlab
  GTdef('nicoya_all_stations_inv.in')

    Output

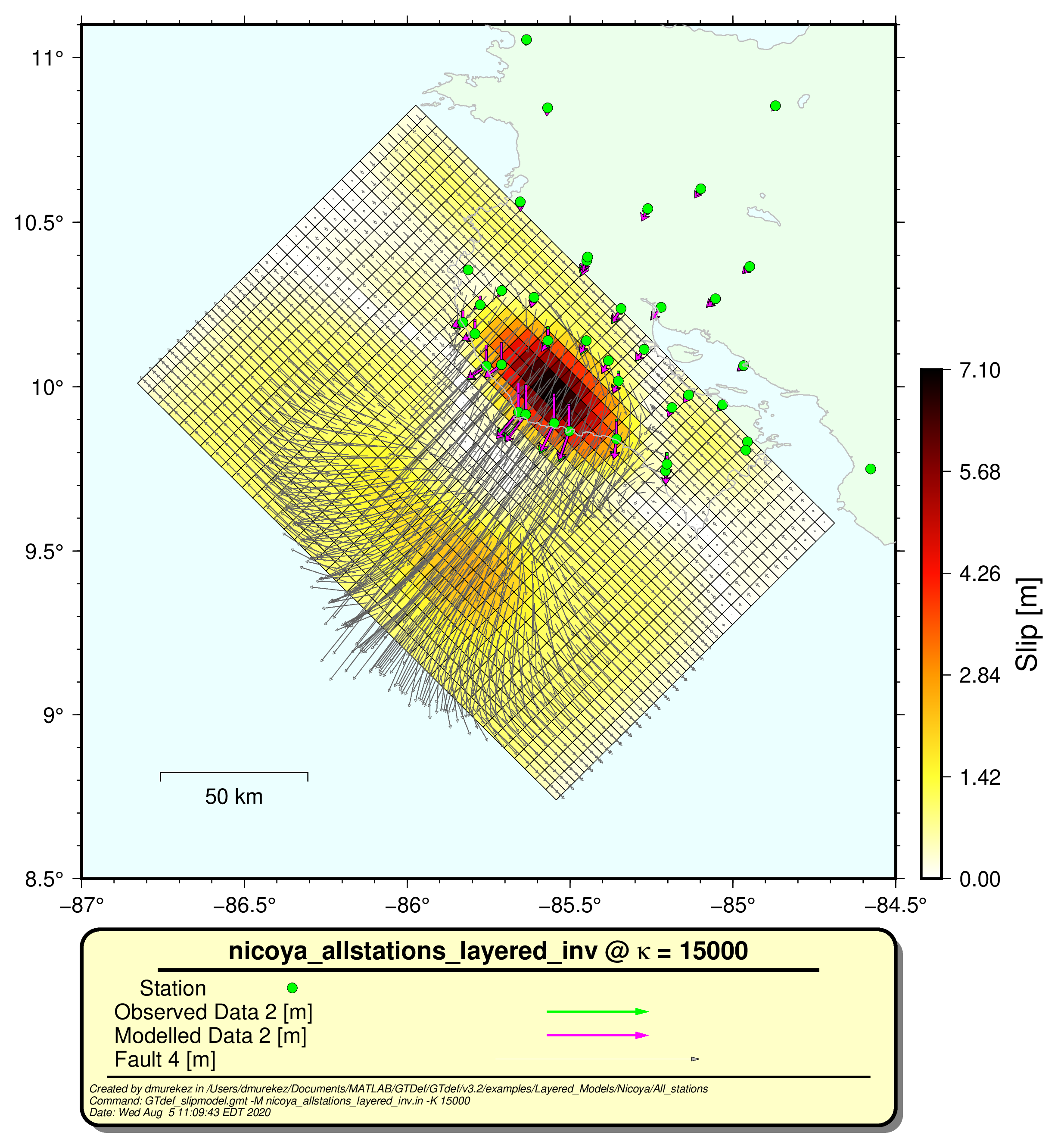
    Since this is set up to run an inversion, the output files will be the same type ('_kp*.out') however it too will create outputs for the algorithms' Green's functions by default. The GTdef_edgrn.m algorithm will generate these and store them in a subdirectory called ./edgrnsfcts. The directory will contain three large files describing each strike-slip (ss), dip-slip (ds), and the compensated linear vector dipole (cl). Once the files are created, you can change the fault and station geometry minding not to go beyond the depth and distance limits established in the earth layered line.

    Plotting results

    Using the gmt plotting programs introduced in the sections above, we can plot the misfit curve and the geographic representation of the slip and deformation estimates. 
      # in shell (command line)
  GTdef_slipmodel.gmt -M nicoya_allstations_layered_inv.in  -K15000 -D
    For the Nicoya Dataset and the layered model, a representative result is shown below.



    For comparison, we include the Okada solution for the same fault geometry and data.

  11. GTdef formats for Green's Functions

    12. (to be completed)

  12. Ingesting External Green's Functions

    13. (from 'examples/Joint_Inversion/3_Tsunami')

    (to be complete)

  13. References:

murekezigatech.edu, anewmangatech.edu | Updated: